Validation Case Study – Resource Allocation

Summary

This table summarizes the differences in forecasting accuracy between PBE’s models and the naïve models across the 118 cells. The table shows the weighted-average absolute percent errors for both models. Scripts were used to weight the errors for each cell.

PBE was able to reduce the naïve model error by 75% . We have undertaken a total of 14 such validation exercises and have in each case reduced the naïve model error by 75% to 85%. In other words, this Case Study is far from our best example. As of this writing, we are aware of no one else being able to reduce the naïve model error at all, much less challenge PBE’s standards.

A Blinded Forecasting Test To Objectively Determine if it is
Possible to Quantify the Relationship Between Amounts of
Details/Samples and Rx’s at the Individual Doctor Level

Call Value Targeting

Introduction

Pharmaceutical companies are constantly focused on improving the productivity of their detailing and sampling. This is not surprising, since an organization’s sales force is normally its second largest expense item after R & D. Additionally, details and samples are such potent generators of Rx’s that the opportunity cost of failing to fully exploit their potential is enormous.

Companies are increasingly relying on mathematical models that their creators claim quantify the relationship between details and samples on the one hand and filled Rx’s on the other, for each individual doctor. In theory, such models could show how 1,000 representatives might detail and sample with the effectiveness of 1,200 or more — without making more calls.

However, there is a question every user of models should want answered: “Do these models really do what they claim to do?” How does a company know if its models actually quantify the cause and effect of personal selling? Specifically, do the models quantify cause and effect well enough so that, if representatives follow the resulting plans, they will be more productive than they would have been on their own?

In order to determine if anyone could actually quantify cause and effect, an interested party sponsored a shoot out among organizations that claim to be able to forecast at the doctor level. The test was designed to determine if anyone could backup their claim. Five organizations agreed, including PBE, and one later dropped out. Other invitees declined to participate from the outset.

PBE won the shoot-out “hands down”. According to the sponsor, none of the other participants was able to account for the impact of details and samples at all! The Validation Methodology Section of this Case Study explains how the sponsor reached these conclusions. In short, they created a placebo.

The sponsor of the shoot-out has released very little detailed information. However, the Case Study that follows presents highly detailed information from a blinded validation test conducted by a leading pharmaceutical company. This exercise involved only PBE, but the protocol was the same as in the shoot-out. This protocol (which was reviewed by a leading academic) enables any company to quickly determine if and how well a model building methodology finds the relationship between numbers of details and samples on one hand and total filled Rx’s on the other at the individual doctor level for an established brand.

Validation Methodology

A pharmaceutical company provided PBE with monthly, doctor-level detailing and sampling data for 30 consecutive months for one of its brands. The company also provided the corresponding doctor-level prescribing data for only the first 24 of those months. PBE’s mission was to tell the company how many Rx’s each doctor had had filled during the remaining six months that were withheld from PBE. This way, the company was able to immediately validate PBE’s forecasts for each doctor by comparing them to the actual audited Rx’s for these same doctors. By taking advantage of existing data, the company was able to avoid the time and expense of a test market – which would also have forced representatives to adhere strictly to specific call plans.

For purposes of analysis, the doctors were grouped into 120 cells. This was done by segmenting the doctors by 12 levels of market share and 10 levels of prescribing volume. Forecasts were made for each doctor within each cell and these forecasts were then summed to produce a single forecast for each cell. The absolute percent difference between forecasted Rx’s and actual Rx’s was calculated for each cell.

The doctors were grouped into 120 cells for two reasons. First, although 120 numbers are a lot to look at, this is far better than looking at forecasts for tens of thousands of doctors. Second, there is a tremendous amount of random variation in the number of scripts individual doctors write for a brand from one period to the next. This variation is primarily due to the luck of the draw in terms of the number of patients showing up in the office that the doctor considers to be appropriate for a specific drug. Grouping the doctors eliminates most of the effect of this random variation.

Prior to the exercise, it was agreed that the accuracy of PBE’s forecasts would be compared to the accuracy of forecasts produced by a naïve model, i.e., the placebo. The naïve model simply stated that each doctor’s filled Rx’s would increase at the national rate. In this case, Rx’s were flat, so the naïve model assumed that each and every doctor’s prescribing would remain constant.

The naïve model assumes, in effect, that detailing and sampling have no impact on filled Rx’s. Both the client and PBE agreed that any methodology that cannot at least beat the naïve model is worthless at best — and counter-productive at worst.

The sponsor of the shoot-out used this naïve model to determine that PBE had indeed quantified the cause and effect of personal selling which none of the other participants was able to do.

TABLES 1- 4

These tables show the period-to-period changes in detailing and sampling for the brand used in the exercise. PBE has had the opportunity to examine the detailing and sampling of scores of brands. We have consistently observed that there is a large amount of period-to-period variation in detailing and sampling at the individual doctor level even when the national numbers are stable. Such was the case with this brand.

This variation in promotion at the doctor level makes the validation protocol discussed earlier a true test of someone’s ability to model cause and effect well enough to create plans that find hidden profits.

Tables 1, 2, 3 compare detailing activities (Primary, Secondary and Reminder) during the forecasted six months (Period 2) versus the previous six months (Period 1) for every doctor who wrote a script or received promotion during either period. For example, Table 1 shows that 3,939 doctors received exactly three Primary Details during Period 1. (This number is shown in the far right column.) Looking across the corresponding row, one sees that of the 3,939 doctors who received 3 primary details in Period 1 — 1,807 were not detailed at all during Period 2. In fact, fewer than 10% (298) of the doctors who received three primary details during Period 1 received that exact same number in Period 2.

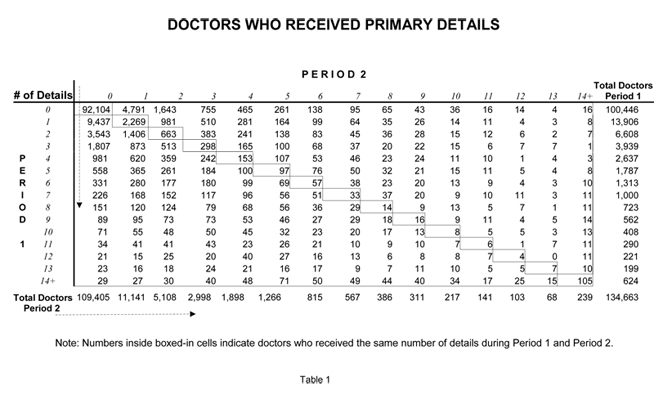
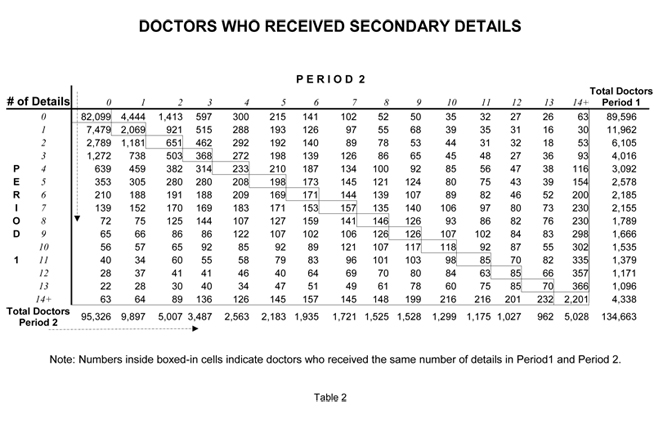
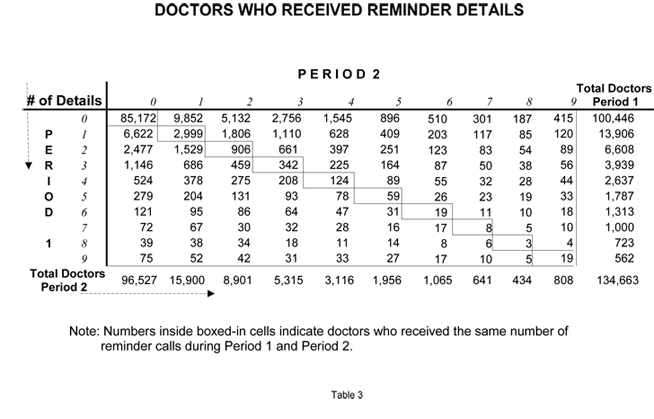
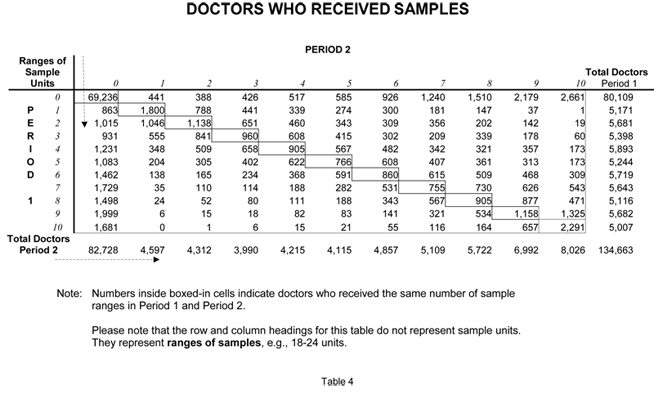
TABLE 5

This table shows the results of PBE’s forecasts versus the naïve model forecasts. For purposes of the exercise, the doctors were grouped 12 ways according to their initial shares and 10 ways according to their prescribing volumes. We then added all the forecasts for doctors within each cell to produce 118 forecasts (2 cells were empty) rather than 134,000 forecasts. The data were looked at the cell level for two reasons. First, grouping the doctors into cells greatly reduces the impact of random variation created by patient visits. Second, aggregating the data makes it much easier to see what was going on.

Here is how to read the table, starting by reading across the first line on Table 5 (CELL 1). This cell has the doctors in the lowest share and volume groups – Group I in both cases. There were 2,404 doctors in this cell and they wrote a total of 2,404 scripts during Period 1. During Period 2, the forecasted period, their scripts jumped to 12,549. PBE had predicted 12,626. PBE’s forecast was off by 0.06%. The naïve model (Period 1 vs. Period 2) which assumed no change, was off by 80%.

 

Results of PBE’s Forecasts vs. Naïve Model Forecasts
				Actual Rx’s	Actual Rx’s	Predicted Rx’s	PBE Error	Naïve Error
Cell	Share Group	Volume Group	Freq	Period 1	Period 2	Period 2	Predicted vs.Actual	Period 1 vs.Period 2
1	1	1	2404	2404	12549	12626	0.00613	0.80843
2	1	2	1659	3904	13352	12640	0.05331	0.70763
3	1	3	596	2611	6574	6810	0.03599	0.60281
4	1	4	408	2743	5611	5878	0.04756	0.51113
5	1	5	245	2393	4466	4197	0.06029	0.46421
6	1	6	236	3340	5045	5590	0.10811	0.33793
7	1	7	178	3927	5425	5069	0.06565	0.27613
8	1	8	107	3790	5294	4742	0.10421	0.28409
9	1	9	25	1414	1734	1393	0.19689	0.18454
10	1	10	5	460	516	388	0.24736	0.10853
11	2	1	1865	1865	6307	6762	0.07215	0.70432
12	2	2	2248	5436	13623	13594	0.00215	0.60099
13	2	3	1328	5887	11813	11094	0.06082	0.50163
14	2	4	1292	8863	14859	14226	0.04260	0.40353
15	2	5	868	8580	13165	13516	0.02670	0.34826
16	2	6	923	13063	18757	17485	0.06781	0.30356
17	2	7	846	18681	23953	23004	0.03959	0.22008
18	2	8	898	32204	39452	37278	0.05511	0.18371
19	2	9	671	40776	45465	43848	0.03557	0.10313
20	2	10	298	33128	35724	33806	0.05368	0.07266
21	3	1	998	998	2819	3015	0.06938	0.64602
22	3	2	1745	4258	8620	8980	0.04170	0.50607
23	3	3	1209	5362	8810	8241	0.06464	0.39138
24	3	4	1450	10080	14061	15698	0.11643	0.28308
25	3	5	1068	10582	13991	13659	0.02374	0.24366
26	3	6	1399	19932	25147	24842	0.01213	0.20740
27	3	7	1237	27294	31880	32440	0.01758	0.14384
28	3	8	1299	47023	53566	52420	0.02139	0.12215
29	3	9	1372	84595	90745	87971	0.03057	0.06778
30	3	10	1417	180655	185594	178636	0.03750	0.02662
31	4	1	948	948	2354	2586	0.09867	0.59726
32	4	2	1308	3192	5928	5870	0.00971	0.46161
33	4	3	1021	4544	6342	6729	0.06101	0.28348
34	4	4	1371	9570	11361	11604	0.02136	0.15772
35	4	5	1033	10193	12157	12310	0.01258	0.16161
36	4	6	1387	19842	22829	22421	0.01786	0.13081
37	4	7	1470	32283	35298	33460	0.05206	0.08542
38	4	8	1467	52945	56969	53180	0.06651	0.07063
39	4	9	1429	88134	91007	84928	0.06680	0.03158
40	4	10	2237	328011	323316	311589	0.03627	0.01452
41	5	1	588	588	1149	1538	0.33828	0.48823
42	5	2	951	2326	4082	3697	0.09436	0.43010
43	5	3	812	3602	4776	5141	0.07633	0.24583
44	5	4	1146	8028	8928	10088	0.12989	0.10089
45	5	5	949	9407	10023	11298	0.12715	0.06145
46	5	6	1310	18850	19577	21193	0.08257	0.03714
47	5	7	1392	30751	31044	30838	0.00664	0.00946
48	5	8	1514	54428	53871	53045	0.01534	0.01034
49	5	9	1321	80697	78533	75885	0.03373	0.02755
50	5	10	2280	376893	358270	347064	0.03128	0.05198
51	6	1	323	323	576	720	0.25070	0.43915
52	6	2	743	1878	2918	3118	0.06875	0.35625
53	6	3	604	2697	3171	2977	0.06114	0.14952
54	6	4	866	6006	6543	6878	0.05122	0.08206
55	6	5	682	6759	6702	7040	0.05047	0.00855
56	6	6	1114	16037	17102	16828	0.01602	0.06227
57	6	7	1242	27607	26499	26773	0.01031	0.04181
58	6	8	1248	44517	42100	41535	0.01343	0.05742
59	6	9	985	59863	55760	54668	0.01957	0.07359
60	6	10	1937	354250	332732	320256	0.03750	0.06467
61	7	1	752	752	1449	1393	0.03892	0.48106
62	7	2	1376	3322	4773	4479	0.06169	0.30412
63	7	3	1107	4939	5542	6121	0.10447	0.10867
64	7	4	1456	10156	9492	10310	0.08621	0.06995
65	7	5	1196	11830	10892	11489	0.05479	0.08609
66	7	6	1817	26007	23952	25236	0.05363	0.08580
67	7	7	1958	43195	38686	39996	0.03386	0.11656
68	7	8	2025	72930	65817	65655	0.00246	0.10809
69	7	9	1651	101016	93518	90301	0.03439	0.08019
70	7	10	2696	523590	488898	475539	0.02732	0.07096
71	8	1	450	450	763	710	0.06958	0.41038
72	8	2	1422	3591	4257	4306	0.01136	0.15665
73	8	3	1333	5941	5475	5587	0.02045	0.08522
74	8	4	1773	12386	10753	10870	0.01088	0.15185
75	8	5	1460	14390	11591	11949	0.03086	0.24147
76	8	6	1962	28239	23687	25043	0.05724	0.19216
77	8	7	2205	48433	41165	41708	0.01318	0.17655
78	8	8	2258	80507	66902	68912	0.03004	0.20335
79	8	9	1682	101828	89116	87985	0.01268	0.14265
80	8	10	2684	588252	538877	525613	0.02461	0.09163
81	9	1	1220	1220	1774	2230	0.25722	0.31224
82	9	2	1658	4065	4445	4488	0.00970	0.08542
83	9	3	1520	6714	5556	5204	0.06320	0.20848
84	9	4	2100	14620	10620	10466	0.01444	0.37671
85	9	5	1454	14307	10565	10696	0.01239	0.35425
86	9	6	1864	26569	19885	20219	0.01678	0.33615
87	9	7	1718	37746	28869	29031	0.00559	0.30749
88	9	8	1630	58176	47091	47927	0.01776	0.23541
89	9	9	1179	71621	58923	58759	0.00278	0.21550
90	9	10	1540	358936	324675	324880	0.00063	0.10552
91	10	2	629	1481	1313	1141	0.13081	0.12841
92	10	3	589	2588	2035	1812	0.10941	0.27178
93	10	4	892	6154	3683	3700	0.00460	0.67086
94	10	5	624	6164	3609	3776	0.04633	0.70781
95	10	6	739	10548	7091	6276	0.11485	0.48755
96	10	7	587	12802	8734	9170	0.04994	0.46576
97	10	8	445	15980	11442	11588	0.01276	0.39662
98	10	9	281	16966	14729	13045	0.11430	0.15188
99	10	10	282	54733	46965	45232	0.03690	0.16540
100	11	2	264	792	662	595	0.10088	0.19617
101	11	3	514	2349	1325	1244	0.06129	0.77269
102	11	4	716	4998	2854	2879	0.00878	0.75113
103	11	5	390	3807	2135	2233	0.04585	0.78334
104	11	6	403	5711	3187	3445	0.08106	0.79198
105	11	7	257	5596	3443	3389	0.01582	0.62529
106	11	8	153	5310	3869	3973	0.02681	0.37243
107	11	9	70	4137	3774	3331	0.11735	0.09619
108	11	10	39	7842	5948	6804	0.14386	0.31843
109	12	1	2986	2986	3443	3270	0.05030	0.13270
110	12	2	3434	8197	5872	5659	0.03626	0.39591
111	12	3	1854	8109	4411	4379	0.00715	0.83859
112	12	4	1710	11724	5267	5292	0.00487	1.22597
113	12	5	823	8063	3929	3927	0.00063	1.05216
114	12	6	591	8127	3822	3813	0.00247	1.12633
115	12	7	186	3935	2012	2099	0.04308	0.95581
116	12	8	68	2288	1222	1396	0.14251	0.87229
117	12	9	14	830	603	540	0.10473	0.37647
118	12	10	5	822	685	710	0.03591	0.20000